I went onto http://gickr.com/ and put my storyboards into GIFs to start to get an idea how they will start to move when they are out into After Effects, all these GIFs only have 5 key frames but from what I have learnt from before my After Effects animations will have more than that.
Friday, 23 December 2011
Silent Movie...GIFs
I went onto http://gickr.com/ and put my storyboards into GIFs to start to get an idea how they will start to move when they are out into After Effects, all these GIFs only have 5 key frames but from what I have learnt from before my After Effects animations will have more than that.
Thursday, 22 December 2011
Patterns...Penrose Tiling
-'A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles. Penrose tilings are named after mathematician and physicist Roger Penrose
who investigated these sets in the 1970s. The aperiodicity of the
Penrose prototiles implies that a shifted copy of a Penrose tiling will
never match the original. A Penrose tiling may be constructed so as to
exhibit both reflection symmetry and fivefold rotational symmetry.'
-'A Penrose tiling has many remarkable properties, most notably:
- It is non-periodic, which means that it lacks any translational symmetry. More informally, a shifted copy will never match the original.
- It is self-similar, so the same patterns occur at larger and larger scales. Thus, the tiling can be obtained through "inflation" (or "deflation") and any finite patch from the tiling occurs infinitely many times.
- It is a quasicrystal: implemented as a physical structure a Penrose tiling will produce Bragg diffraction and its diffractogram reveals both the fivefold symmetry and the underlying long range order.'
-Penrose's second tiling uses quadrilaterals called the "kite" and "dart", which may be combined to make a rhombus. However, the matching rules prohibit such a combination. Both the kite and dart are composed of two triangles, called Robinson triangles, after 1975 notes by Robinson.
- The kite is a quadrilateral whose four interior angles are 72, 72, 72, and 144 degrees. The kite may be bisected along its axis of symmetry to form a pair of acute Robinson triangles (with angles of 36, 72 and 72 degrees).
- The dart is a non-convex quadrilateral whose four interior angles are 36, 72, 36, and 216 degrees. The dart may be bisected along its axis of symmetry to form a pair of obtuse Robinson triangles (with angles of 36, 36 and 108 degrees), which are smaller than the acute triangles.
These rules often force the placement of certain tiles: for example, the concave vertex of any dart is necessarily filled by two kites. The corresponding figure (center of the top row in the lower image on the left) is called an "ace" by Conway; although it looks like an enlarged kite, it does not tile in the same way. Similarly the concave vertex formed when two kites meet along a short edge is necessarily filled by two darts (bottom right). In fact, there are only seven possible ways for the tiles to meet at a vertex; two of these figures – namely, the "star" (top left) and the "sun" (top right) – have 5-fold dihedral symmetry (by rotations and reflections), while the remainder have a single axis of reflection (vertical in the image). All of these vertex figures, apart from the ace and the sun, force the placement of additional tiles.
-The third tiling uses a pair of rhombuses (often referred to as "rhombs" in this context) with equal sides but different angles. Ordinary rhombus-shaped tiles can be used to tile the plane periodically, so restrictions must be made on how tiles can be assembled: no two tiles may form a parallelogram, as this would allow a periodic tiling, but this constraint is not sufficient to force aperiodicity, as figure 1 above shows.
There are two kinds of tile, both of which can be decomposed into Robinson triangles.
- The thin rhomb t has four corners with angles of 36, 144, 36, and 144 degrees. The t rhomb may be bisected along its short diagonal to form a pair of acute Robinson triangles.
- The thick rhomb T has angles of 72, 108, 72, and 108 degrees. The T rhomb may be bisected along its long diagonal to form a pair of obtuse Robinson triangles; in contrast to the P2 tiling, these are larger than the acute triangles.
There are 54 cyclically ordered combinations of such angles that add up to 360 degrees at a vertex, but the rules of the tiling allow only seven of these combinations to appear (although one of these arises in two ways).
-Starting with a collection of tiles from a given tiling (which might be a single tile, a tiling of the plane, or any other collection), deflation proceeds with a sequence of steps called generations. In one generation of deflation, each tile is replaced with two or more new tiles that are scaled-down versions of tiles used in the original tiling. The substitution rules guarantee that the new tiles will be arranged in accordance with the matching rules. Repeated generations of deflation produce a tiling of the original axiom shape with smaller and smaller tiles.
Patterns...MC Escher Tessellations
The most famous artist to use tessellation in there work is Mc Escher, here is a collection of some of his works.
Patterns...Tessellation
-'A Tessellation (or Tiling) is when you cover a surface with a pattern of flat shapes so that there are no overlaps or gaps.'
-'Tessellation is the process of creating a two-dimensional plane
using the repetition of a geometric shape with no overlaps and no gaps.
Generalizations to higher dimensions are also possible. Tessellations
frequently appeared in the art of M. C. Escher, who was inspired by studying the Moorish use of symmetry in the Alhambra tiles during a visit in 1922. Tessellations are seen throughout art history, from ancient architecture to modern art.
In Latin, tessella is a small cubical piece of clay, stone or glass used to make mosaics.The word "tessella" means "small square" (from "tessera", square, which in its turn is from the Greek word for "four"). It corresponds with the everyday term tiling which refers to applications of tessellations, often made of glazed clay.'
-'In 1619 Johannes Kepler
did one of the first documented studies of tessellations when he wrote
about the regular and semiregular tessellation, which are coverings of a
plane with regular polygons. Some two hundred years later in 1891, the
Russian crystallographer Yevgraf Fyodorov
proved that every periodic tiling of the plane features one of
seventeen different groups of isometries. Fedorov's work marked the
unofficial beginning of the mathematical study of tessellations. Other
prominent contributors include Shubnikov and Belov (1951); and Heinrich Heesch and Otto Kienzle (1963).'
-'A regular tessellation is a highly symmetric tessellation made up of congruent regular polygons. Only three regular tessellations exist: those made up of equilateral triangles, squares, or hexagons. A semiregular tessellation
uses a variety of regular polygons; there are eight of these. The
arrangement of polygons at every vertex point is identical. An edge-to-edge tessellation
is even less regular: the only requirement is that adjacent tiles only
share full sides, i.e. no tile shares a partial side with any other
tile. Other types of tessellations exist, depending on types of figures
and types of pattern. There are regular versus irregular, periodic
versus nonperiodic, symmetric versus asymmetric, and fractal tessellations, as well as other classifications.'
-'Penrose tilings using two different polygons are the most famous example of tessellations that create aperiodic patterns. They belong to a general class of aperiodic tilings that can be constructed out of self-replicating sets of polygons by using recursion.'
-'A monohedral tiling is a tessellation in which all tiles are congruent. Spiral monohedral tilings include the Voderberg tiling discovered by Hans Voderberg in 1936, whose unit tile is a nonconvex enneagon; and the Hirschhorn tiling discovered by Michael Hirschhorn in the 1970s, whose unit tile is an irregular pentagon.'
-'Basaltic lava flows often display columnar jointing as a result of contraction
forces causing cracks as the lava cools. The extensive crack networks
that develop often produce hexagonal columns of lava. One example of
such an array of columns is the Giant's Causeway in Northern Ireland.
The Tessellated pavement in Tasmania is a rare sedimentary rock formation where the rock has fractured into rectangular blocks.
Within botany, the term "tessellate" describes a checkered pattern, for example on a flower petal, tree bark, or fruit.'
Top Ten...Patterns
I have decided to pick the subject of patterns for my top ten brief, I have started by finding definitions about patterns.
Wednesday, 21 December 2011
Time Line Workshop
(Insert images of work here)
It is also giving us time to devlop our drawing skills, we all need to have good enough drawing skills to show our ideas on paper in a clear way, its no good being a genious on a mac if you can't draw your ideas first.
We had a discussion about the pros and cons of working with time lines, somethings that kept coming up were the editing possibilities. Working with timelines gives you the option to visualise the storyboard and then move frames around if they don't work in the order they are in.
It gives you the skills to start thinking about your animation over time and how long each frame will last for and also to start thinking about the parts of the animation when nothing really happens.It is also giving us time to devlop our drawing skills, we all need to have good enough drawing skills to show our ideas on paper in a clear way, its no good being a genious on a mac if you can't draw your ideas first.
Storyboard Crit
(insert images of work here)
We had a small crit in pairs on our storyboards we have drawn up, we had to look at each others and explain what we though was going on in each storyboard.
It made me realised what I had missed out in my storyboards, often things that were obvious once they had been pointed out.
Tuesday, 13 December 2011
After Effects Session 3
-Keyframe interpolation and Using Illustrator Paths.
-Interpolation- To insert between fixed points.
The pen tool in After Effects is exactly the same as the pen tool in Illustrator.
When you create key frames it creates busier curves.
When you use convert vertex tool on the pen tools it creates straight lines for the shape to follow.
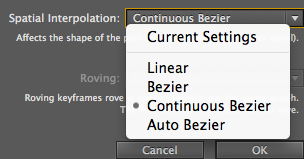
You can also change the interpolation by going to Animation-> Key frame interpolation and changing the spacial interpolation.
We are going to change these key frames to Hold Keyframes.
We select all the keyframes and go to...
These are the visible changes...
This means there is no interpolation, there are no in between frames. It holds the frame there until the next key frame.
Using Illustrator Artwork.
If you change the opacity key frames and toggle hold keyframe the word blinks on and off.
If you press the ALT key you can compress and expand all your keyframes at once.
We have selected the middle key frames.
If you change the roving to rove across time it keeps the selected key frames relevant to each other and to the first and last key frames. It keeps the key frames at a constant speed.
Using Illustrator-
We created a vector shape in Illustrator and copied it into After Effects.
The shape then follows the motion path copied from Illustrator.
This reverses the direction of the key frames so if you want it to move from clockwise to anti-clockwise this is how it would be done.
You can change the orientation to the layer to move relevant to the path.
Masks-
You Must select your layer and then make a shape on that layer, it makes parts of the layer opaque and parts transparent.
You can change the masks feathering-
You can turn the masks on and off.
Like in Illustrator you can change the shape of the mask with the anchor points.
You can also create a mask by using the pen tool to make the shape you want.
Here I have used the mask extension tool to revel a word.
Using masks we can make a word appear to melt.
Using a Matte-
This is a process of using a layer to specify what parts of another layer we can see.
This is one of the animations I made in todays session.
Subscribe to:
Comments (Atom)